Using the Fibonacci Sequence when Designing Quilts

Quilting with Fibonacci: OK, who or what is Fibonacci? Fibonacci, whose real name might have been Leonardo Bigollo, was a mathematician who lived in Italy about 1170 – 1240. His father was a merchant and it is thought that young Leonardo traveled with him. In his travels, he learned about the Hindu-Arabic number system. This system made accurate calculations more easily than the existing Roman Numerals system. Fibonacci wrote a book about this system and its advantages around 1202, in which he introduced the Fibonacci sequence among other formulas.

Of course, he didn’t call it that and, honestly, he didn’t invent it. The idea had been around for a while and was well known in nature. You’ve probably seen it, in fact, in flowers, cabbages, succulents, or a Nautilus shell. Fibonacci is a mathematical sequence often depicted as a spiral.

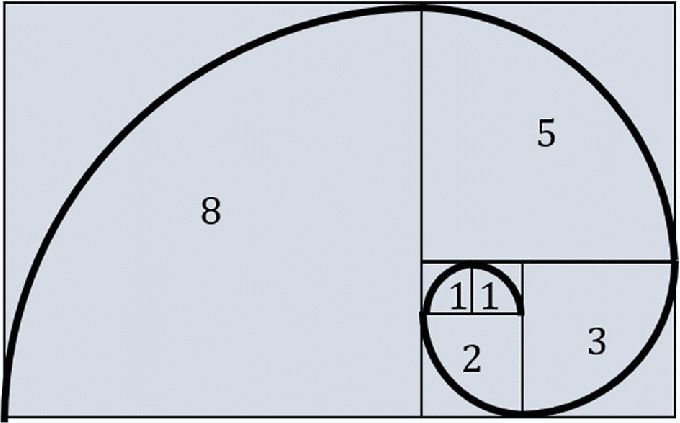
In mathematics, the Fibonacci numbers form a sequence such that each number is the sum of the two previous numbers starting from 0 and 1. For example, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. How does this relate to quilting? Let’s check it out!

A Fibonacci Quilt Block

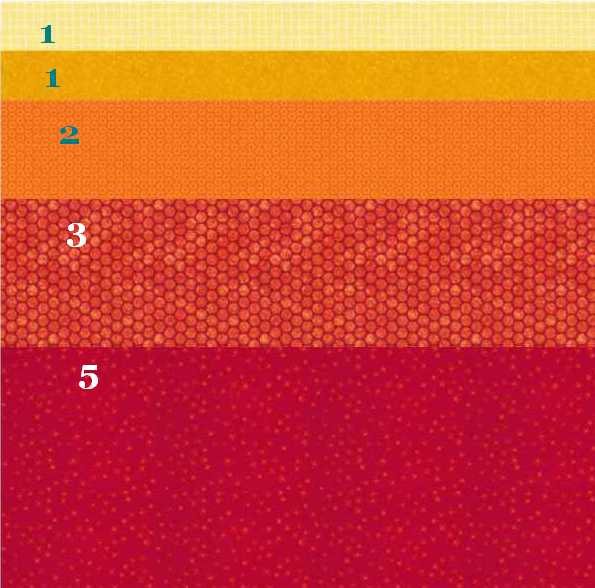
Let’s think about making a quilt block as an example of Fibonacci. Here is a 12″ block that shows the Fibonacci sequence. I skipped the 0 in the sequence and started with 1. A 1″ strip plus a 1″ strip = 2″. So my next strip is 2″ wide. To figure the width of the third strip, I added that 2″ to the previous 1″ strip and got 3″. So the next strip is 3″ wide. To figure the fourth strip, I added that 3″ with the 2″ to get 5″. And so on.

These numbers are arbitrary. I could have made an 18″ block by starting with a 1-1/2″ strip. Or I could have started with an 8″ wide strip, making the next one 13″ and the one after that 21″. That would make a big block!

What can you do with this block? Here are two 16-block quilts:

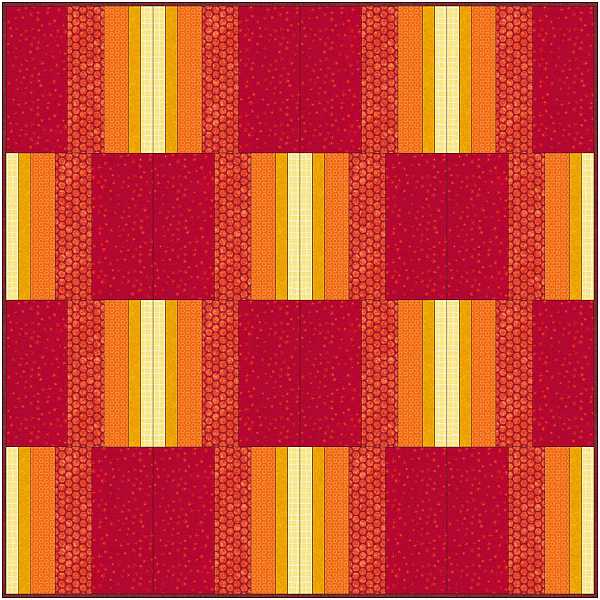
Or, you can make one huge modern quilt like this one:

I really wanted to do a bargello quilt, but this was as close as I could come. It’s a horizontal row quilt, with the first row being 2″ wide, the second is 2″ wide, the third is 4″ wide, and so on through the Fibonacci sequence.

Can you piece a Fibonacci block?

Of course! For example, a 5″ x 5″ square block could be divided into (2) blocks using the Fibonacci sequence: a 2″ x 5″ rectangle and a 3″ x 5″ rectangle. Carole Lyles Shaw  discusses this a little more on her website.

Let me play with that a bit. How about these blocks, pieced using the Fibonacci sequence:

These quilts make your eyes blur, don’t they? They might be better in calmer colors like this one done in patriotic colors. 

Or this one:

Kat and Cat Quilts had another take on this design. You can see her quilt here. 

Let’s take that same block and put it together so there is a four-patch in the middle.

Jinny Beyer had some other examples of this in her article Fibonacci and the Golden Ratio. 

Where else can you use Fibonacci in quilts?

How about in a border ratio? The Fibonacci sequence of 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 could be used to determine border size. Here I have started with the lightest color (the lime green) and kept darkening fabrics as I went around the panel.  The quilt finished at 72″ x 92″. The borders are 2″, 2″, 4″, 6″, 10″ – yes, they fit the sequence.

How can you use the Fibonacci spiral in quilting?

Why not make a backing – or another modern quilt? Here is a quilt that is pieced using the spiral I showed you at the top of this page. What would this look like if you made two of these and sewed them together, one with the purple on top and one with the purple on the bottom? What would it look like if you took those two blocks sewn together and added one of the blocks below on both sides?

You could actually put the spiral in there, like this one by Kate Henderson.  Or this one by My Colorqueue  that put the circles back to back.

You could use Fibonacci to determine the size of applique circles like this one at Nana’s Nahwelt .

The possibilities of using Fibonacci in quilting are endless!

Subscribe